Unit 3 Sections 4

Home

Online Grapher

Hyperglossary

Unit 3 Polynomials and Rational Functions

Graphing Calculator Skills needed for this chapter.

Section 3.4 Fundamental Theorem of Algebra

This section explores one of the most important and famous algebraic theorems.

Objectives: You should be able to:

Understand the concept of multiplicity

Find the exact zeros of a polynomial

Basic steps( assuming one at least one rational):

Graph
Check graph and table feature for any integer or rational zeros that can be easily verified
List all possible rational zeros, check graph for these.
Use table feature on ASK to substitute all possible rational zeros.
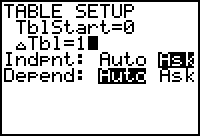
Use synthetic division to reduce equation to a more solvable one
Solve reduced equation, remembering that imaginary and irrational zeros come in pairs.

Find the least polynomial given the zeros

Section 3.5 Rational functions .

This section explores functions in the form f(x) = p(x)/q(x). For help on graphing look at section 3.6 in the text and on this page below.
You should be able to:

Find the Domain and range of rational functions.

This can be done easiest with the graphics calculator.
y = 1/x
The x values in the range are from negative infinity to positive infinity excluding zero. This is the Domain written in interval notation as (-oo , 0) U (0, oo) . The range is also all the reals except 0 written as , (-oo , 0) U (0, oo) .
y = (2x+1) / ( x+1)
The domain is all the reals except 0 and the range is all the reals except 2.
D= (-oo , 0) U (0, oo) R = (-oo , 2) U (2, oo).

Find the Asymptotes of rational functions using algrbaic rules and with the calculator..: There are three possible type of asymptotes to rational functions, vertical, horizontal and slant.
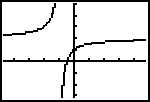: This function has both a horizontal and a vertical asymptote.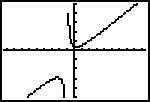; This function has a slant asymptote.; To find the asymptote,use long division to divide the denominator into the numerator. The quotient without the remainder is the slant asymptote when degree of numerator is 1 more than that of denominator.

Section 3.6 Graphing Rational Functions

This section explores the graphs of rational functions.

You should be able to find the following using the graphics calculator along with a combination of algebraic methods:

x and y intercepts

Symmetry

Horizontal, Vertical, and Slant asymptotes

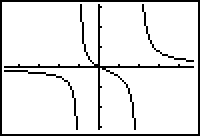graph The function on the left has vertical asymptotes at x = 2 and x = -1. It has horizontal asymptote at y = 0.

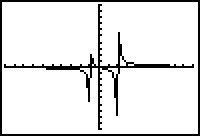
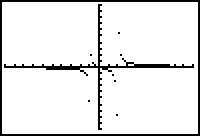
Use the excellent examples in the text to help you with this section. In graphing rational functions the author suggests using DOT MODE on the calculator. This works for some functions and eliminates the "false asymptote" that the calculator can give you. However a better graph can be obtained in many functions using ZOOM ZDecimal after pressing GRAPH. Another alternative is to double the ZDecimal Window as shown.

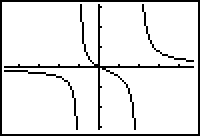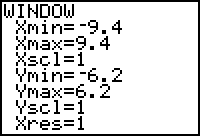*Adjusting the view screen for rational f(x) = x / (x²-x - 2*)

Using ZOOM 6	Using Dot mode	Using ZDecimal	Zdecimal doubled

Explore rational functions with LiveMath below.

Top

Proceed to Unit 4