Online Grapher
Hyperglossary
Unit
4 - Exponential and Logarithmic Functions
This chapter focuses on exponential and logarithmic functions and their application to real life problems.
![]() Graphing Calculator Skills needed
for this chapter.
Graphing Calculator Skills needed
for this chapter.
Section 4.1 Exponential Functions and their Graphs
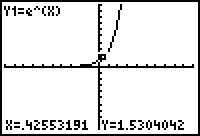 This section
explores functions in the form of y = ax similar to the graph
on the left.
This section
explores functions in the form of y = ax similar to the graph
on the left.
Highlights and Objectives :
Evaluate exponential functions on the calculator. The symbol ^ on the calculator is used for exponents.
3^4 = 34 = 81
Apply properties of exponents to simplify exponential functions. 34 *35 = 39.
Identify and evaluate functions with the natural exponential function with base e.
Graph exponential functions and identify asymptotes.
Apply exponential function to real life problems including compound interest.
Click on the LiveMath symbol to further explore exponential graphs
Section 4.2 Logarithmic Functions
This section explores the inverse of the exponential function, the logarithmic function, y = logax
Highlights and objectives
Understand the definition of Logarithms including the natural log, ln
Evaluate logarithmic expression.
Use the properties of logarithms on Page 331 to evaluate and simplify logarithmic expressions.
Find the domain and range of logarithmic functions.
Sketch the graphs of logarithmic functions.
![]() Click
on the LiveMath logo to explore logarithmic
graphs
Click
on the LiveMath logo to explore logarithmic
graphs
Section 4.3 Properties of Logarithms
This section explores the algebraic properties of logarithms which are use in later math for simplification. The calculator is used very little, if at all, in this section.
Highlights and Objectives:
Apply the change of base formula.
Rewrite the Logarithm of a Product and of a Quotient.
Condense a logarithmic expression.
log( x + 2) + log ( 2x - 3)
= log[(x + 2)(2x-3)]
Use the properties and definitions to evaluate logarithms without a calculator.
Ex 74 page 346
|
log4 2 +
log432 answer is 3 |
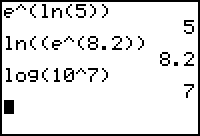
Using the special properties of Logarithms and exponential functions to simplify and evaluate expressions
log (10b ) = b 10log c = c
ln (eb ) = b elnc = c
Click on the LiveMath logoto further explore logartihmc properties online.
©Joan Bookbinder 1998 -2002 All rights reserved
