Graphing Calculator Skills needed for this chapter.

---

Section 6.1  Matrices and Systems of Equations

Highlights and Objectives :

Determine the order of a matrix.
Identify a particular element of a matrix.
Be able to rewrite a system of equations into an augmented matrix.
Perform elementary row operations with and without the graphics calculator .
            (Note the blue box on the bottom of page 460 for help with this topic)
Solve a system of linear equations using Gaussian Elimination

Note: the ref key on the TI83 MATRIX->MATH scroll to ref
(This function will do all the elementary row operations automatically )
You should, however, be able to determine the solution by backwards substitution
once the matrix is reduced.

                                 

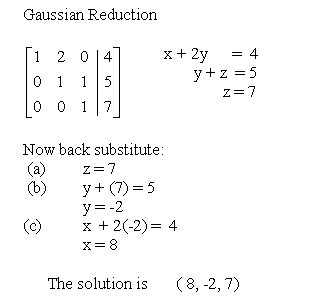
Solve a system of linear equations using Gauss - Jordan Elimination

Note: the rref key on the TI83
MATRIX->MATH scroll down to rref
(This function will do all the elementary row operations automatically.)
You should, however, be able to determine the solution to the system once the matrix is reduced.

Examples of solutions from reduced matrices:

Section 6.2 Operations with Matrices

Highlights and Objectives

Equality of matrices
Identity Matrices
Matrix Multiplication
Addition, Subtraction, and Scalar Multiplication of matrices  

 

Experiment NOW with the values in the embedded LiveMath Notebook below.

Section 6.3 Inverses of Square Matrices

Highlights and Objectives

Find the inverse of a square matrix.

To find the inverse algebraically, a method similar to Gauss Jordan must be used. You are looking for a matrix A such that A-1A equals the Identity matrix. On the calculator it can be done step by step or just by using the A-1 button. You are responsible just for finding them on the calculator. TRY IT NOW!!!!!  Use your calculator now to find the inverse of: .

Use inverse matrices to find solution to systems with unique solutions
        X = A^-1B.

Click on the LiveMath w Image to Explore Inverse Matrices

  Test Yourself


Top