Assignment

Section 3-6

Unit 5   Systems of Equations and Inequalities

This chapter focuses solving systems of equations and inequalities using algebraic and graphical methods.

  Graphing Calculator Skills needed for this chapter.

Section 5.1 Solving Systems Using Substitution and Graphical methods

Highlights and Objectives

The substitution method in this section goes into much more detail than may have been covered in a previous course. The basis of this method is to :

1. Solve one of the equations for one variable in terms of the other.
2. Then substitute the expression found in 1 to obtain an equation in one variable
3. Solve the new equation
4. Substitute that answer back into the equation found in step 1.
5. Check your work

The substitution method can be used also with nonlinear problems, though not all problems can be easily algebraically solved.

Click on the LiveMath icon to explore substitution.

 Applications to Systems.

There are many examples in the text and on the CD ROM of real life applications.

Graphical method finding points of intersection

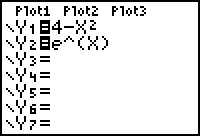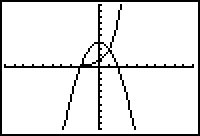Enter the functions in the y editor	GRAPH, ZOOM 6	2nd CALC 5
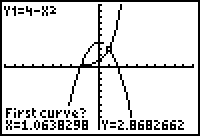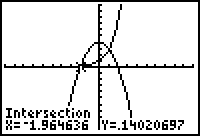Cursor to the first graph, press ENTER, 2nd graph ENTER, then ENTER again after moving cursor near intersection	First point of intersection	Repeat process for 2nd point of intersection

Section 5.2 Elimination Method and interpretations of solutions.

The elimination method may also have been covered in a previous course however not in such depth and not with non linear functions.

Highlights and Objectives

Elimination method

1. Obtain coefficients that differ only in sign by multiplying all terms of one or both equations by suitably chosen constants.
2. Add the equations to eliminate one variable
3. Solve for that variable
4. Substitute the solution from step 3 into either equation to find the solution of the other variable.
5. Check your solutions either algebraically or graphically.

Interpretations of Graphs. Graphs of two linear equations have either one, none, or infinitely many points of intersection. This determines how many solutions a system may have. Some systems are called inconsistent if they have no solution.

   

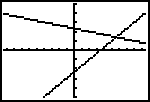
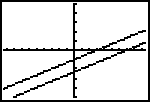
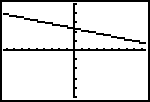
Programming the calculator for finding a solution to a system of linear equations. Page 404 has a program for finding the solution to a linear system, given it is a unique solution.

Explore non-Linear Systems

This worksheet may take a while to load. Please be patient.
This worksheet explores the algebraic method along with the graphical method.

Test Yourself   before continuing

  Top

Sections 3 - 6

©Joan Bookbinder 1998 1999 All rights reserved