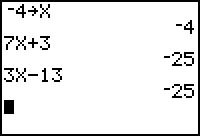Unit 2 Section 1- 3

Unit 2 - Intercepts, Zeros, and Solutions

This chapter focuses on solving many different types of equations, both algebraically and graphically. Many of these methods were covered in the prerequisite courses for this class. However, we will also be exploring ways to solve many of these equations with the TI graphics calculator.

Graphing Calculator Skills needed for this chapter.

Section 2.1 & 2.2 Linear Equations and Modeling

Though the author labels Section 2.1 "Linear Equations", there are many examples in this section that are NOT linear. Please try to differentiate between those fitting the linear format and those that do not.

Main points and objectives:

An Equation

is a statement that two algebraic expressions are equal. Finding the solution or solutions to an equation is the primary focus of this chapter. Two types of equations mentioned here are conditional equations and identities . These can be further explored on page 168. Another type of equation is a contradiction. A contradiction has NO solution at all.

The validity of an equation can be tested using the logic functions of the calculator in the TEST Menu. Store the value of x. Then, on the home screen, type in the equation. If it is true, the calculator returns a value of 1. If the statement is not true, then the calculaotr returns a value of 0.

A Linear equation

is an equation in one variable. This variable can be x, y, z, or any other letter. Most of the problems in this chapter use the variable x. It is also easier to use that on the graphing calculator. The standard form for a linear equation is

ax + b = 0

where a, b are real numbers and a not equal to 0. Sometimes a linear equation does not resemble the formula above but can be manipulated using the rules of algebra into that form.Use the LiveMath Notebok below to explore.

Equations with Extraneous Solutions.

Even when an equation is solved according to all the rules of algebra, it is possible that the solution does not satisfy the equation. [Image]

In the above example, what happens when x=2 is substituted back into the equation?

Sections 2.1 - 2.2
4 Methods to check your algebraic work with a calculator -

1) Example # 26 on page 176
7x + 3 = 3x - 13

In solving this algebraically, the answer is -4
To check this on the calculator, store x as -4,
( -4 STO x ENTER) then type in both sides
of the equation pressing ENTER after each one.

2) Use the TEST Menu as described above The 1 means that the equation is true with 4 as x.

3) Another way of checking the work is to graph both sides and use the calculator's intersection program. This is explained in section 2.2 and on both the CD ROM and video. Here is a brief synopsis of the method. Use 2nd CALC 5 to find the x value at the intersection.This method does require some juggling with the viewing window as is seen in the third display below.

TRY it now!! Use your graphing calculator and 2nd CALC 5 to solve:
3x - 7 = 5x - 19 for x. Adjust the standard window for Ymax = 25

Standard Form
4) This is another way of solving equations on the calculator. Set the equation equal to zero then enter on the calculator. Use 2nd CALC 2 to find the zero.

In the fourth display you can also see how the use of the table can help to find the solution or to check an answer.
You can also use a program like LiveMath to solve and check your work.Change some of the values in the first line to see how different problems produce different solutions

Section 2.3 Complex Numbers

This should have been covered to some degree in a previous course. Use this section as a refresher. However, for those of you who have the TI 83 many of these exercises can be done on that calculator. Press the MODE button and scroll down to the next to the last line. Move the cursor to a+ bi and press ENTER. Then press CLEAR. You will now be able to work with imaginary numbers accurately. The i is above the decimal point on the calculator

Top